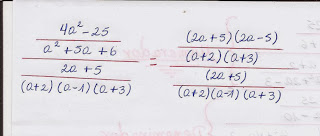Matematicas :Miguel Angél Monserrate: noviembre 2013

lunes, 25 de noviembre de 2013

Función Cuadratica

Este tipo de funciones tiene como característica que cuando a>0 el vértice de la parábola en la parte inferior de la misma, cuando a<0 el vértice se encuentra el la parte superior.

Concavidad de la función

En la función cuadrática, f(x) = ax2 + bx + c, el coeficiente (a) indica si la parábola es cóncava hacia arriba o hacia abajo.

Método de Sustitución

Es el método para resolver ecuaciones algebraicas sustituyendo una variable con una cantidad equivalente de términos de otras variables de manera que el numero total de incógnitas se reduzca.

Pasos para realizar el método de sustitución.

Se despeja la misma incógnita en ambas ecuaciones.

Se igualan las expresiones, con lo que obtenemos una ecuación con una incógnita.

Se resuelve la ecuación.

El valor obtenido se sustituye en cualquiera de las dos expresiones en las que aparecía despejada la otra incógnita.

Los dos valores obtenidos constituyen la solución del sistema.

EJEMPLO

Despejaremos Incógnitas

1. Aquí vamos a intercambiar términos y resolver el ejercicio planteado.

2.Ya en este paso vamos a despejar la incógnita de x y nos queda así ya con la respuesta.

3.En este ultimo paso despejaremos ( y ) luego obtenemos el resultado de las incógnitas.

4.Aquí vamos a intercambiar términos y a resolver el ejercicio planteado.

Ecuaciones por el método de igualacion

Método de igualación

Este método consiste en una pequeña variante del antes visto de sustitución.

Para resolver este método de ecuación hay que despejar una incógnita, la misma en las dos ecuaciones e igualar el resultado de ambos despejos con lo que se obtiene una ecuación de primer grado.

EJEMPLO DE ESTE MÉTODO

1. Aquí tenemos el ejercicio planteado para proseguir a resolverlo.

2. Luego pasamos a despejar las incógnitas que son (x) (y) y sacar el resultado que se pide

3.Ya puestos los términos en sus respectivos lugares pasaremos a resolverlos

4. Aquí tenemos el despeje de (y) y su respectiva respuesta que salio del despeje 

5. Luego tenemos para despejar la (x) e intercambiamos valores y nos da la respuesta del despeje de (x)

6. Y
 ya para ver si da el resultado igualamos términos con los despejes de 
(y) y (x) y nos da la respuesta del ejercicio que es igual al planteado.

Esta
 ya es la respuesta del ejercicio y nos quedo igual al planteado con lo 
que empezamos al principio, ya que como su nombre lo dice es de 
igualación.

FUNCIONES LINEALES

Una función lineal
 es una función polinomica de primer grado, es decir , 
una función cuya representación en el plano cartesiano es una linea 
recta. Esta función se puede escribir como; donde ( m y b ) son 
constantes reales; ( y, x )es una variable real. 

REPRESENTACIÓN GRÁFICA 

Se despeja la función.
Se constituye una tabla de colores, basta con dos planos.
Se unen los puntos por una linea recta, prolongándola de tal modo que este representada en todo el plano.

Pasos necesarios para representar gráficamente una función

Hasta
 ahora sabíamos representar las funciones elementales utilizando las 
propiedades de estas, pero ya estamos en condiciones de representar 
cualquiera

Se las puede representar siguiendo estos pasos:

Dominio
Punto de corte en los ejes
Signo de la función
sintonas y ramas infinitas
Monotonía y extremos relativos
Curvatura y puntos de inflexión

domingo, 24 de noviembre de 2013

Trabajos Autonomos de noviembre.

Repaso de el deber de Ecuaciones Numéricas

EJERCICIOS QUE PRACTICAMOS:

a) 2 - x - 1/3=4

- x – 1/3 = 4 – 2

-x – 1= 4 – 2(3)

-x -1 = 4 -6

-x= 4 – 6 + 1

-x= 5 – 6

(-1) – x= - 1(-1)

X= 1

b) 2x – 2= x/3 + 3

3(2x) – 3(2)= 1(x) + 3(3)

6x – 6= x + 9

5x= 15

X= 15/ 3

X= 3

jueves, 14 de noviembre de 2013

martes, 12 de noviembre de 2013

lunes, 11 de noviembre de 2013

DIFERENCIAS DE DOS BINOMIOS

DIFERENCIAS DE DOS BINOMIOS.

El cuadrado de la suma de dos monomios es igual al cuadrado del primero, mas el doble producto del primero por el segundo, mas el cuadrado del segundo monomio.

TRINOMIO

El producto de dos binomios de esta forma que tienen un termino comun es igual al cuadrado del termino comun mas la suma de los terminos no comunes multiplicando por el termino comun mas el producto de los terminos comun.

CUBO DE LA DIFERENCIA DE DOS BINOMIOS

el cubo de diferencia de dos monomios es igual al cubo del primer monomio, menos el triple del cuadrado del cuadrado del primero por el segundo, mas el triple del primero por el cuadrado del segundo, menos el cubo del segundo monomio.

EJERCICIOS...

TRABAJO AUTONOMO 3

domingo, 10 de noviembre de 2013

TRABAJO AUTONOMO 2

MULTIPLICACION DE POLINOMIOS

MULTIPLICACION DE POLINOMIOS

El producto de los polinomios que se obtiene multiplicando el polinomio multiplicando por cada termino del polinomio multiplicador y sumando los productos parciales.

RECOMENDACIONES PARA MULTIPLICAR POLINOMIOS

1: Se completa y ordenan los polinomios con respecto a una sola letra o variable (en forma descendente); un caso falte un término, este se completa con un cero.

2: Se multiplican cada uno de los términos del multiplicando por lo del multiplicador y en cada resultado obtenido, se desplaza un termino con la intención que las expresiones aparezcan en forma ordenada, para luego reducir términos semejantes.